Compute ASTC
[TOC]
前言
ASTC格式作为当前最新的gpu纹理格式，有很多的优势：
-
对纹理尺寸无要求，支持alpha
-
较新的Android和IOS都支持
-
纹理精度与压缩比特率多级可调节，可以选择block大小从4x4到12x12，相应的比特率从8bpp到0.89bpp
但目前只有离线压缩工具（ARM ASTC-encoder， Intel的ISPC），压缩过程很慢，关键是游戏中运行时生成的纹理，就无法利用压缩贴图了。
为此，研究用computershader进行实时的纹理压缩，首先我们的目标是对LDR的2D纹理，选取block大小为4x4和6x6，通过分析ASTC纹理压缩的原理和参数搜索过程，鉴于ASTC纹理格式本身复杂，可选参数又极多，对参数搜索等进行一些必要的简化，去掉耗时大精度提升有限的搜索，利用computeshader的高度并行性，在运行时实时地进行纹理的ASTC压缩编码，在压缩纹理精度上达到可接受，在压缩速度上保证实时，并尽可能提高速度，提升精度。
基于块的有损压缩原理
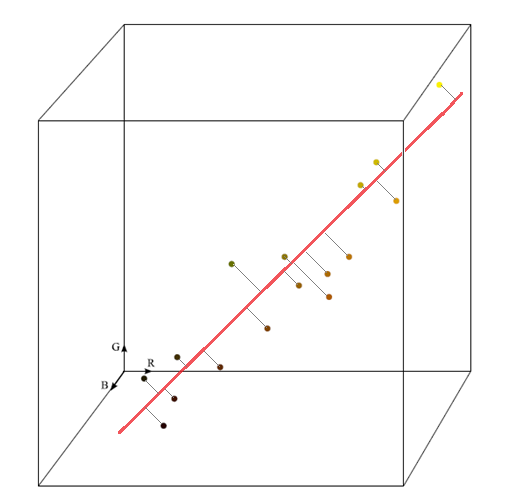
基于块的有损压缩算法基于颜色的局部相关性假设，把像素看作是RGB/RGBA空间中的点，在这个空间中找一个线段，其他所有像素都用这个线段的两个端点（称为endpoints）的插值来表示。
- 一个块内的颜色值比较少，可以拟合到RGB空间的一个直线上。
- 但是这种单线性拟合对于有些情况来说，质量损失严重。举个最简单的例子，如果一个4×4的 block中包含红色、蓝色、绿色的三个像素，只用一个线段插值压缩后必然会有个颜色精度丢失很大。
- BC7引入了像素子集划分的思路，把块内的像素集分成多个子集，每个子集独立选出一个线段进行像素插值。像素子集的划分，称为partition。
ASTC的改进
-
ASTC也是一种基于块的有损压缩算法，提供了4x4到12x12的多种块大小，每个Block块都压缩为固定的128bit，不同的块大小就对应于不同的压缩率。
-
ASTC沿用了BC7的partition，但是增加到了最多可以划分成4个子集，就有划分成2个子集，3个子集，4个子集，共三种情形，每种情形有1024种划分方式，总共3072种划分方式，相对于BC7的64种Partition复杂了很多。编码时用2个bit存partition count-1，10个bit存partition index。
-
ASTC提出的有界整数序列压缩(BISE bounded integer sequence encoding)，更紧凑的整数序列编码，可以达到分数级的bit per value。正是由于有了这个特性，才使得ASTC能有广泛的不同级别的压缩比特率。
ASTC的搜索参数空间大小估算
- Partition数量：3072 + 1
- DualPlane：2
- 合法的Blockmode种类：占用11bit，2048的量级
- color endpoint modes(CEM)字段：multi partition情况下占6bit，single partition情况下占4bit 总的搜索量级：3073 * 2 * 2048 * 16 = 201392128 ~ 约2亿量级
ASTC压缩的精度损失来源分析
ASTC压缩的精度损失主要来自下面三个方面：
-
基于主轴进行颜色插值的插值误差
处在主轴线上的点是可以被精确插值的，离主轴距离为d的点，插值误差即可由d来衡量。
-
endpoints的量化误差
量化Range为\(R\)，256个像素级，量化分配到\(R\)个值上，形成\(R-1\)个像素范围，平均每个像素级范围大小为\(\lceil256/(R-1)\rceil\)，取范围中心进行反量化，则像素量化误差为：\(\lceil256/(R-1)\rceil/2\)，随着R越小，误差越大。
例如：量化范围\(R=48\)时，对颜色值\(c = 8\)进行量化，再反量化后，颜色值还原为5，误差为3。用\(Range=256\)的话，就相当于无损失的量化了。
-
weights的量化误差
量化Range为\(R\)，那么权重\(w(0 \leq w \leq 1)\)的量化误差为：\(\vert w - [wR+0.5] / R \vert\) ，由于\(w*R\)与\([w*R+0.5]\)相差最多0.5，因此误差最大值是\(0.5/R\)，随着R越小，误差越大。
-
weights网格的插值误差
除了3d纹理的z方向上外，权重网格在各个对应维度上可以小于实际的块大小。用双线性插值来拟合。
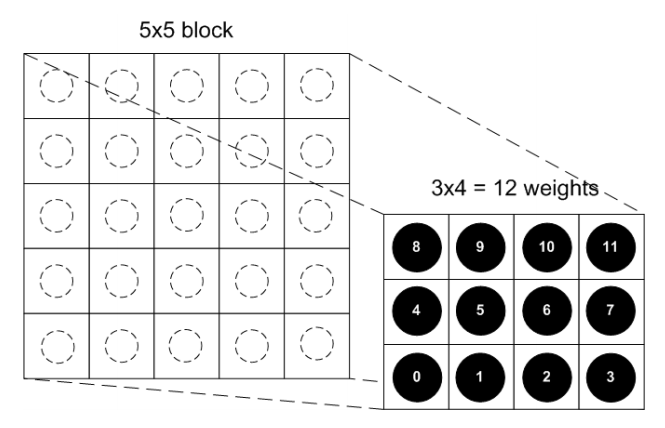
ASTC块的编码组成
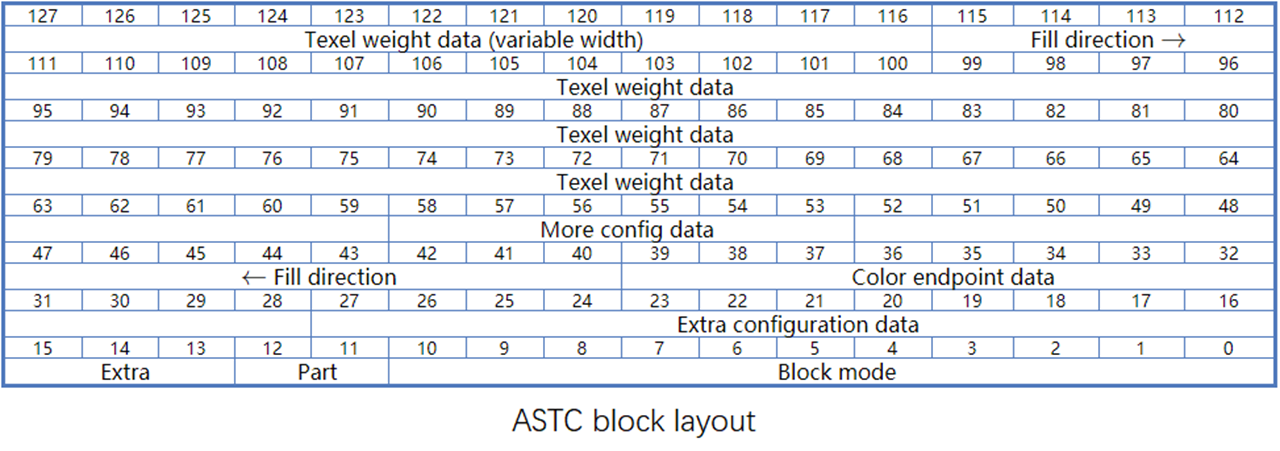
- 开始的bit数据是配置数据
- endpoints颜色数据在配置数据之后。
- 128bit里，weights数据在尾部，按bit位倒着排列。
- weights和endpoint数据占用多少位是不固定的，取决于blockmode和整个128bit的分配，总体而言weighs占用bit越多，endpoint占用bit就越少，反之亦然。就是要找到一个最优的bit分配。
block mode的组成
-
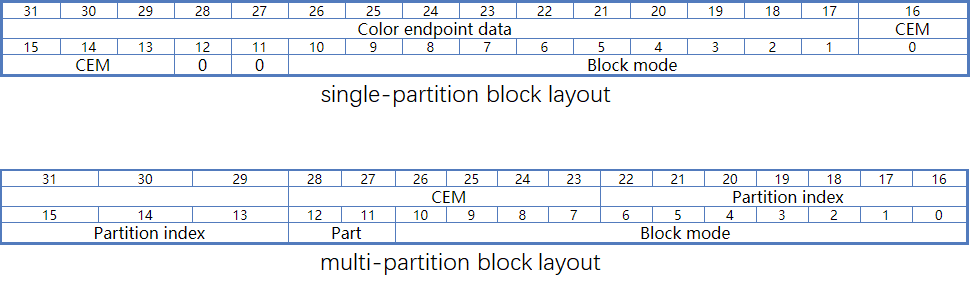
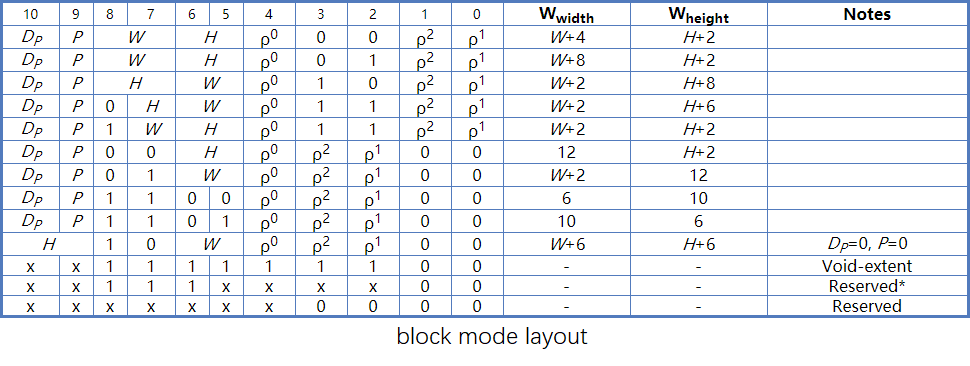
blockmode是位于128bit的最开头的固定的11bit。
-
Blockmode里定义了权重weights的量化范围，权重网格的大小。
由权重量化范围，间接决定了endpoints的量化范围。根据整个128bits减去weights的编码占用和其他配置占用后剩余的bits位数可以确定endpoints的bit位数。
single partition & multi partition
\(\quad\quad\)基本就是根据像素在block内的坐标，通过固定的hash函数生成partition划分。block越大，越有可能要划分multi partition。对于一个block，如何选取划分为几个子集，划分为怎样的子集，才有更好的压缩精度，ARM-ASTC有先对像素聚类，但基本上还是在穷举搜索各种partition。
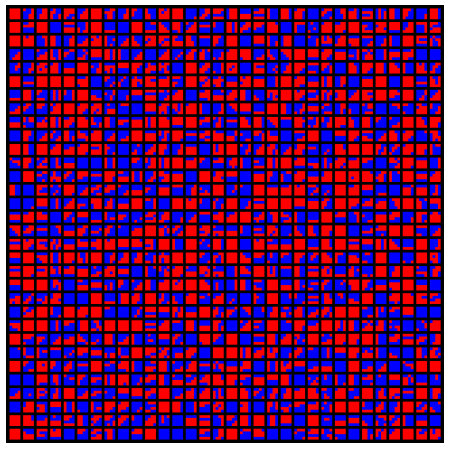
block 4*4的所有1024个2-Partition的样式
Benchmark图像
| 含有红绿蓝三色的4x4的图像 | 使用single partition方式压缩 | 使用2-partition方式压缩 |
|---|---|---|
 |
 |
 |
dual planes
- BlockMode Layout里有个D字段，表示是否像素的rgba通道中有任何通道要进行分开编码，也就是会有两套endpoints和权重网格。这一般是由于像素中含有互相不太相关的通道，比如NormalMap，透明遮罩等。
- Partition划分对DualPlanes的各个通道是相同的，也就是分离的两部分通道是属于同一个Partition，有相同的Partition Index。
- dual plane需要两套endpoints和权重数据，占用bits位数要更多，但是另一方面，由于把不相关的通道分离了，那每个Plane里的像素相关度就很高了，可以找出更精确的endpoints。 那是否采用dual plane就取决于压缩精度需要，ARM-ASTC把两种情况都纳入了参数搜索尝试，对此进行精度比较，取最优的方式。
ARM-ASTC离线压缩的大致步骤
- 选取划分
- 对每个划分子集计算endpoints
- 将划分里的像素表示为endpoints的插值，计算插值权重weights。
- endpoints量化，BISE编码
- weights量化，BISE编码
- 组装为128bit块
在上述过程中进行划分集的搜索，权重网格大小的搜索，endpoints / weights的量化范围的搜索
ComputeASTC的简化考虑
- 基于性能开销考虑，不做partitions搜索
- 只用Block4x4、6x6
- 权重网格用4x4的大小
- 对于Block4x4就没有权重网格插值误差了
- 只进行权重weights的量化范围的搜索
- 忽略dual plane，color endpoint modes的搜索
纹理压缩的精度指标PSNR
endpoints的计算
对比了4种方法：
-
Pixel pair with max euclidean distance（Waveren:Real-Time_DXT_Compression）：计算具有最远距离的一对像素点。
-
BoundingBox：取像素点集包围盒的对角线作为主轴方向。（boundingbox仅仅取决于少数最外面的像素点，丢失统计信息）
-
Max accumulation pixel direction（from ARM-ASTC）：减去平均值偏移后，累加rgba各个方向的像素，然后取长度最大的向量的方向作为主轴方向。
-
PCA：将RGB/RGBA数据从3/4维降低到1维。
用PCA计算endpoints
PCA原理
\(\quad\quad\)讲PCA原理的资料很多，从数据分析角度，就是数据降维。而从几何角度来看，从RGB三维降到一维，就是要在像素RGB空间中找一个主轴方向，使得所有像素到这个轴的距离平方和最小。
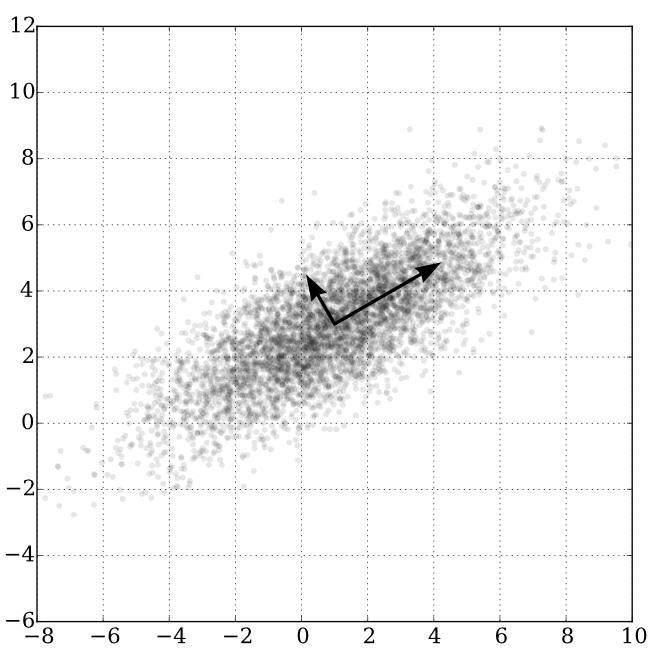
PCA过程
- 去均值化
- 先计算像素平均值，然后减去平均值。
- 计算协方差矩阵
- 把rgb/rgba看作是3/4个随机变量，把block4x4内的像素值看作16个rgb/rgba数据样本，计算协方差矩阵（3x3 或者 4x4）
- 计算协方差矩阵的最大特征值对应的特征向量
- 这可以使用幂次法，用矩阵反复多次乘一个非零的初始向量，然后归一化得到。
- 计算endpoints
- 最大特征值对应的特征向量就是主轴方向，把原像素减去均值后，往主轴方向投影，获取投影方向上的有向距离坐标，取对应坐标最大的和最小的像素作为endpoints，同时对这个坐标归一化后，就是后续需要存储的像素的权重了。
pixels weights
- weight grids：除了3d纹理的z方向上外，权重网格宽高数目可以小于等于像素网格，小于时，会使用双线性插值。
- 权重数据要先进行归一化，再进行量化。
- 权重量化level的确定：level越大精度越高，但会占用更多bit位，影响颜色量化编码，影响颜色值精度。
- weights序列化顺序：逐像素按width, height, depth顺序。
quantization
- 量化就是用尽可能少的bit位去表示给定的数据。
- quantization level
1. weights quantization
- 权重量化过程：将weights数据从归一化的浮点值，映射到整数值。
- [0 ~ 1] 的weights * quantization level -> integer > 查找权重量化表得到最终量化值
2. color quantization
- 颜色量化level的确定：endpoints_quant是根据整个128bits减去weights的编码占用和其他配置占用后剩余的bits位数来确定的。
- 颜色量化过程
- 不同的color endpoint modes(CEM)有不同的编码方案，确定CEM后，再根据量化level，查找颜色量化表。
blockmode搜索
blockmode搜索的主要目的是选取最优的endpoints和weights量化级别。通过先压缩再解压，取误差最小的组合。
| No Alpha：CEM_LDR_RGB_DIRECT | Has Alpha：CEM_LDR_RGBA_DIRECT | ||
|---|---|---|---|
| 权重范围 | Endpoints范围 | 权重范围 | Endpoints范围 |
| QUANT_3 | QUANT_256 | QUANT_3 | QUANT_256 |
| QUANT_4 | QUANT_256 | QUANT_4 | QUANT_256 |
| QUANT_5 | QUANT_256 | QUANT_5 | QUANT_256 |
| QUANT_6 | QUANT_256 | QUANT_6 | QUANT_256 |
| QUANT_8 | QUANT_256 | QUANT_8 | QUANT_192 |
| QUANT_12 | QUANT_256 | QUANT_12 | QUANT_96 |
| QUANT_16 | QUANT_192 | QUANT_16 | QUANT_48 |
| QUANT_20 | QUANT_96 | QUANT_20 | QUANT_32 |
| QUANT_24 | QUANT_64 | QUANT_24 | QUANT_24 |
| QUANT_32 | QUANT_32 | QUANT_32 | QUANT_12 |
// candidate blockmode uint4(weights quantmethod, endpoints quantmethod, weights range, endpoints quantmethod index of table)
#define BLOCK_MODE_NUM 10
static const uint4 block_modes[2][BLOCK_MODE_NUM] =
{
{ // CEM_LDR_RGB_DIRECT
uint4(QUANT_3, QUANT_256, 3, 7),
uint4(QUANT_4, QUANT_256, 4, 7),
uint4(QUANT_5, QUANT_256, 5, 7),
uint4(QUANT_6, QUANT_256, 6, 7),
uint4(QUANT_8, QUANT_256, 8, 7),
uint4(QUANT_12, QUANT_256, 12, 7),
uint4(QUANT_16, QUANT_192, 16, 6),
uint4(QUANT_20, QUANT_96, 20, 5),
uint4(QUANT_24, QUANT_64, 24, 4),
uint4(QUANT_32, QUANT_32, 32, 2),
},
{ // CEM_LDR_RGBA_DIRECT
uint4(QUANT_3, QUANT_256, 3, 7),
uint4(QUANT_4, QUANT_256, 4, 7),
uint4(QUANT_5, QUANT_256, 5, 7),
uint4(QUANT_6, QUANT_256, 6, 7),
uint4(QUANT_8, QUANT_192, 8, 6),
uint4(QUANT_12, QUANT_96, 12, 5),
uint4(QUANT_16, QUANT_48, 16, 3),
uint4(QUANT_20, QUANT_32, 20, 2),
uint4(QUANT_24, QUANT_24, 24, 1),
uint4(QUANT_32, QUANT_12, 32, 0),
}
};
权重的量化范围确定后，Endpoints的量化范围就可以根据剩余的bit位来确定下来。通过计算各个可能的权重量化范围，计算得到上面的这个表。
分有无alpha，对每一个endpoints和weights权重范围组合，进行一次压缩和解压，计算压缩误差，取误差最小的组合。这个明显是很影响时间性能的。在fast版本里，我们就避免做这个搜索了。固定的blockmode带alpha为QUANT_6, QUANT_256，不带alpha为QUANT_12, QUANT_256。
固定的blockmode带alpha和不带alpha分别的量化级别是：
color_endpoint_mode = CEM_LDR_RGBA_DIRECT;
weight_quant = QUANT_6;
endpoints_quant = QUANT_256;
和：
color_endpoint_mode = CEM_LDR_RGB_DIRECT;
weight_quant = QUANT_12;
endpoints_quant = QUANT_256;
bounded integer sequence encoding(BISE)
BISE是编码有界整数序列的高效无损算法，充分利用了整数的有界性。对于有界整数序列，指定了整数范围后，就确定了编码后的总bit位数。对于\(S\)个有界整数的序列，根据数据范围，归类到下面三种模式：
| 压缩模式 | 整数范围\(R\) | 对\(S\)个整数压缩后的bit数 |
|---|---|---|
| Binary | \([0, 2^n-1]\) | \(n*S\) |
| Base3 | \([0, 3 * 2^n-1]\) | \(n*S + \lceil 8S/5 \rceil\) |
| Base5 | \([0, 5 * 2^n-1]\) | \(n*S + \lceil 7S/3 \rceil\) |
按组编码，Base3为每5个数一组（Base5为每3个数一组），每个数会被分成高位和低位，高位组合编码，低位直接存储。高位和低位的分割只取决于数据范围Range。下面的数组每行的第一列即表示那个Range下，高低位bit的分割位置。
const uint8 bits_trits_quints_table[QUANT_MAX][3] = {
{1, 0, 0}, // RANGE_2
{0, 1, 0}, // RANGE_3
{2, 0, 0}, // RANGE_4
{0, 0, 1}, // RANGE_5
{1, 1, 0}, // RANGE_6
{3, 0, 0}, // RANGE_8
{1, 0, 1}, // RANGE_10
{2, 1, 0}, // RANGE_12
{4, 0, 0}, // RANGE_16
{2, 0, 1}, // RANGE_20
{3, 1, 0}, // RANGE_24
{5, 0, 0}, // RANGE_32
{3, 0, 1}, // RANGE_40
{4, 1, 0}, // RANGE_48
{6, 0, 0}, // RANGE_64
{4, 0, 1}, // RANGE_80
{5, 1, 0}, // RANGE_96
{7, 0, 0}, // RANGE_128
{5, 0, 1}, // RANGE_160
{6, 1, 0}, // RANGE_192
{8, 0, 0} // RANGE_256
};
压缩思路
对于数值范围在[0~N)的整数序列，如果N是2的幂，那么每个数就用[logN]个bit去表示就好了。但是如果N是2的幂超了那么一点点呢，就很浪费了。于是考虑把这样的N用\(3*2^n\) 或者\(5x2^n\)的形式来表达，相当于是在两个相邻的2的幂的范围内再找了两个中间的点，比如在64和128之间，有\(5*2^4 = 80\), \(3*2^5 = 96\)。这样浪费就可能会少很多。
举个例子：考虑编码5个范围在[0,2]的整型数据，naive的想法是每个数据用2bit，5个数需要10bit，BISE的想法是每个数据有3可能，5个数排列的话总共有(\(3^5 = 243\))种可能，用8bits的就可以存储所有的这些组合了，每个数据仅需要(8/5=1.6bit)。
BISE的压缩过程
- 确定压缩模式:Base3或者Base5或者Binary
- 确定高低位分割位置
- 分组编码 按组编码，Base3为每5个数一组（Base5为每3个数一组），每个数会被分成高位和低位，高位组合编码，低位直接存储。高位和低位的分割只取决于数据范围Range。
BISE编码表
bits_trits_quints_table数组的每行的第一列即表示那个Range下，高低位bit的分割位置。第二列和第三列表示是用Base3还是Base5编码。
/**
* Table that describes the number of trits or quints along with bits required
* for storing each range.
*/
static const uint bits_trits_quints_table[QUANT_MAX * 3] =
{
1, 0, 0, // RANGE_2
0, 1, 0, // RANGE_3
2, 0, 0, // RANGE_4
0, 0, 1, // RANGE_5
1, 1, 0, // RANGE_6
3, 0, 0, // RANGE_8
1, 0, 1, // RANGE_10
2, 1, 0, // RANGE_12
4, 0, 0, // RANGE_16
2, 0, 1, // RANGE_20
3, 1, 0, // RANGE_24
5, 0, 0, // RANGE_32
3, 0, 1, // RANGE_40
4, 1, 0, // RANGE_48
6, 0, 0, // RANGE_64
4, 0, 1, // RANGE_80
5, 1, 0, // RANGE_96
7, 0, 0, // RANGE_128
5, 0, 1, // RANGE_160
6, 1, 0, // RANGE_192
8, 0, 0 // RANGE_256
};
比如，在序列4,78,55中，大于78的最小的满足三种格式的数分别是：2^7=128; 3∗2^5=96; 5∗2^4=80，其中80为最小，所以可以使用RANGE_80基于5的BISE，RANGE_80决定了共有7bit，高低位分割位置为4。 这三个数的二进制表示为｛000 0100, 100 1110, 011 0111｝，高三位的组合为｛000，100，011｝，低四位的组合为｛0100, 1110, 0111｝，而这3个高三位bits序列中的最大值是4，最小值是0，所以这高三位bits最多有5种情况，那么这3个高三位bits的排列组合总共可能有5^3=125种组合情况，这样的话就可以使用7bits的空间来存储这个组合，将原来需要3∗3=9bits的数据存储在7bits中，进而达到压缩的目的。余下的3个低四位的数据是直接存储，拼接在一起的，经过BISE编码后的bit序列为: {110, 11100111, 01010100}
结合论文[Nystad.2012]来理解arm: astc-encoder的BISE实现代码
以论文里举例N为12时，表达为\(3*2^2\)，用base3的方式压缩，每5个数为一组，因为数都在\(3*2^2\)范围内，所以每个数X都可以表示为：\(X = t * 2^2 + b1 * 2 ^1 + b0 * 2 ^ 0\)，这里的t取值{0，1，2}，对应arm: astc-encoder代码中的highpart， b1，b0取值{0, 1}, 对应代码中的lowpart，如果N更大的话，对应于\(3*2^n\)，就有更大的n，那这里就有更多的lowpart（b0, b1, b2, …）。
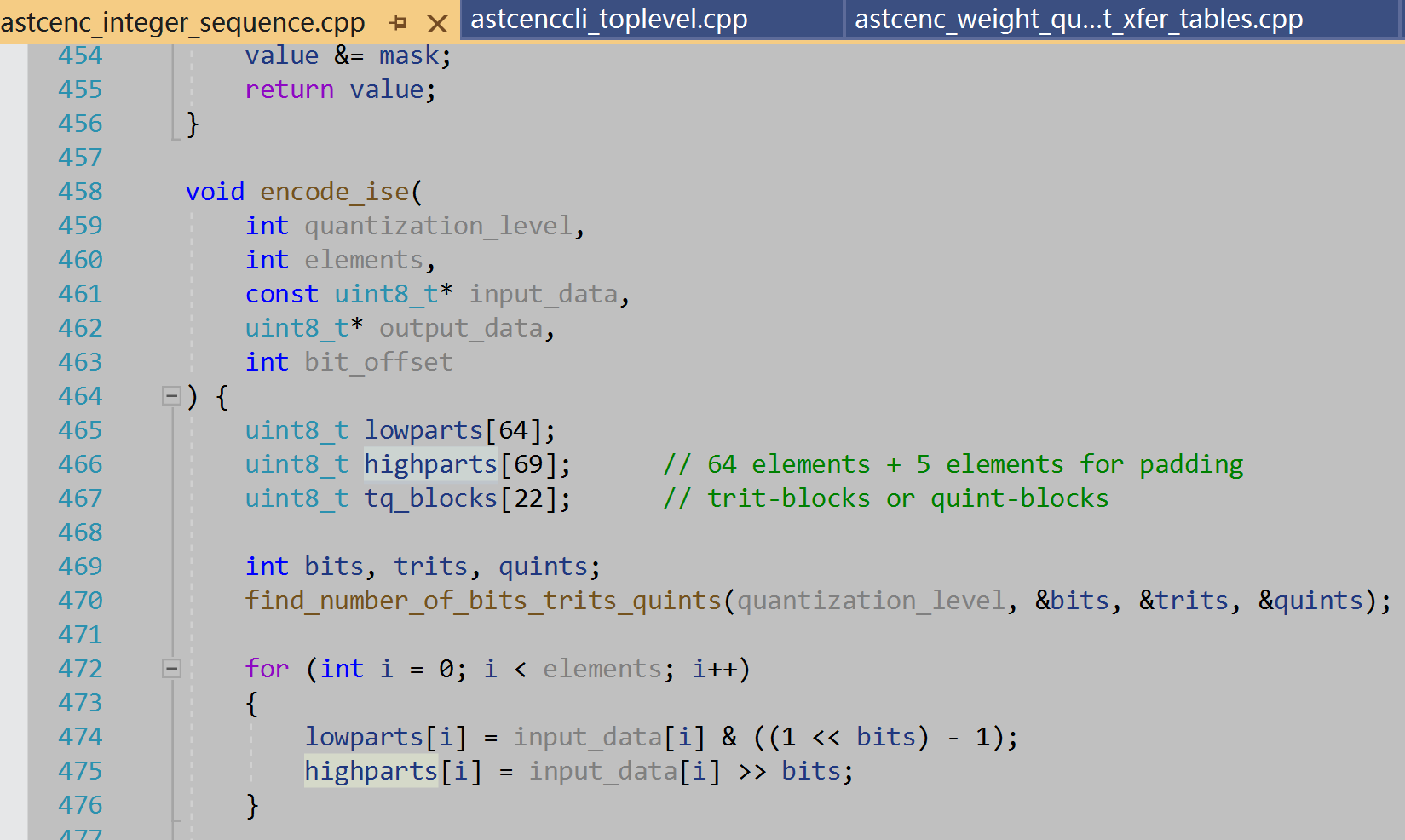5个这样的数表达出来，就有5个t，分别叫t4, t3, t2, t1, t0吧，b1b0合一起2个bit，用B表示吧，B也有5个，叫做B4, B3, B2, B1, B0吧。 t4, t3, t2, t1, t0组成一个3进制5元组，排在一起总共\(3^5 = 243\)种可能，可以用8bit存下来，这个8bit数和3进制5元组是一对一的关系，arm的astc-encoder中的
// packed trit-value for every unpacked trit-quintuplet
// indexed by [high][][][][low]
static const uint8_t integer_of_trits[3][3][3][3][3] = {
编码表integer_of_trits就是从这个3进制5元组到这243个数的映射。
// unpacked trit quintuplets <low,_,_,_,high> for each packed-quint value
static const uint8_t trits_of_integer[256][5] = {
而编码表trits_of_integer就是反过来，从这243个数到3进制5元组的映射。
BISE编码的时候，先通过integer_of_trits把highpart的t4, t3, t2, t1, t0编码为8bit数据（记为T[7~0]），再把T和lowpart的数据交错排列编码。论文里这个红框部分应该是末尾漏掉了B0。
T[7] B4 T[6:5] B3 T[4] B2 T[3:2] B1 T[1:0] B0 这个交错排列对应于代码里
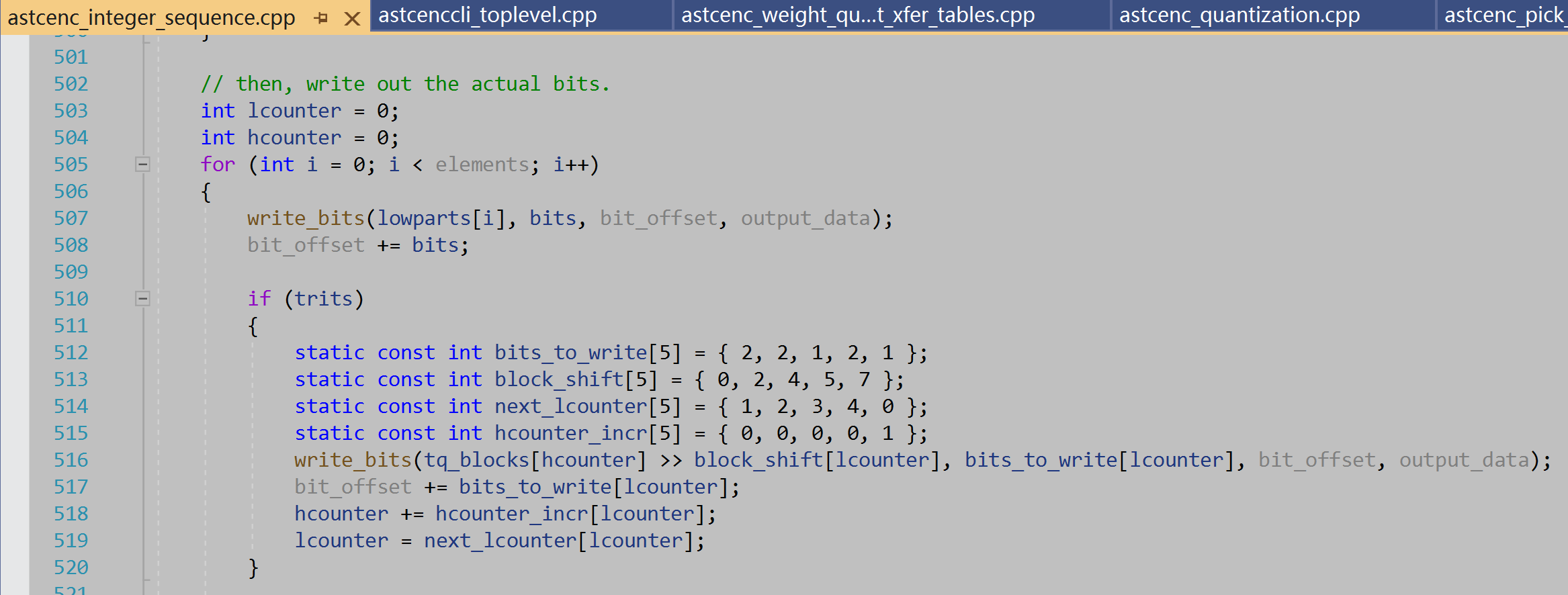
tq_blocks[hcounter] » block_shift[lcounter] ，block_shift[5] = { 0, 2, 4, 5, 7 } 就是bit位偏移量，结合bits_to_write[5] = { 2, 2, 1, 2, 1 }，就是对应取T的 T[1:0], T[3:2], T[4], T[6:5], T[7]
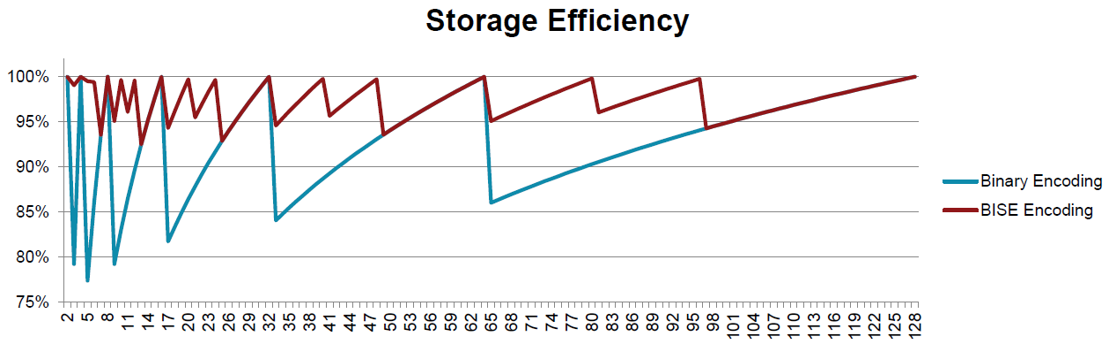
BISE有着接近信息熵的bit编码效率
每个整数需要的bit数 (BitPerValue)：\(B=(n*S + \lceil 8S/5 \rceil) / S\) 或者 \(B=(n*S + \lceil 7S/3 \rceil) / S\)，随着S越大取极限的话，分别趋近于8/5 或者7/3，接近于信息熵\(\log_2{3}\)和\(\log_2{5}\)。
bit的信息量编码效率： \(S\)个范围在\(R\)内等概率分布的正整数，每个正整数的信息量为：\(I=\log_2{R}\)，那么每个bit的信息量：\(I/B = (\log_2{R}) / B\) 下图横轴为整数范围，纵轴为每个bit的信息量
ComputeShader
- 一个thread处理一个block，避免thread间冲突需要同步
*thread数目 thread数目(numThreads的乘积) 有最大值限制 (kernel threadgroup size limit)。 而且GPU一次Dispatch会调用64（AMD称为wavefront）或32（NVIDIA称为warp）个线程（这实际上是一种SIMD技术），所以，numThreads的乘积最好是这个值的整数倍。
*group数目 一个group里的thread数目由shader里的宏定义；Dispatch出的group数目由纹理大小，按一个thread处理一个astc的block来计算确定。 group尺寸的分配需要考虑纹理采样的cached友好性。Optimizing Compute Shaders for L2 Locality using Thread-Group ID Swizzling
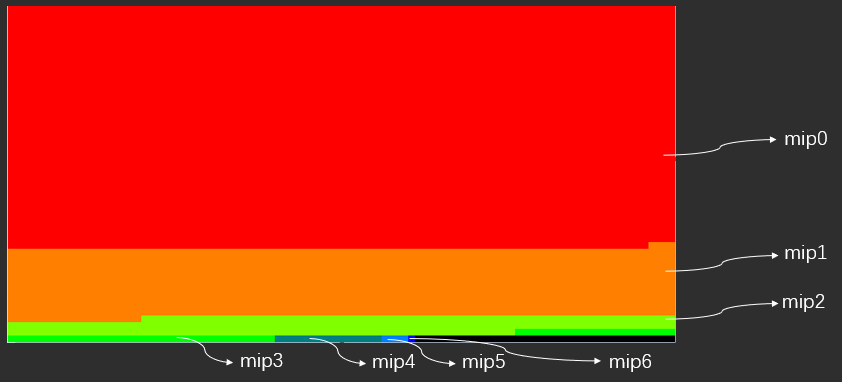
纹理mips合并batch
- 把纹理各级mips合并为一个batch
实验结果
4x4和6x6的实际压缩精度
1. 单图
| Origin | ARM fast 4x4 PSNR: 37 |
|---|---|
 |
 |
| ComputeASTC4x4 PSNR: 34.22 | ComputeASTC6x6 PSNR: 29.34 |
|---|---|
 |
 |
| “ARM fast 4x4” - “Origin” | “ComputeASTC4x4” - “Origin” | “ComputeASTC6x6” - “Origin” |
|---|---|---|
 |
 |
 |
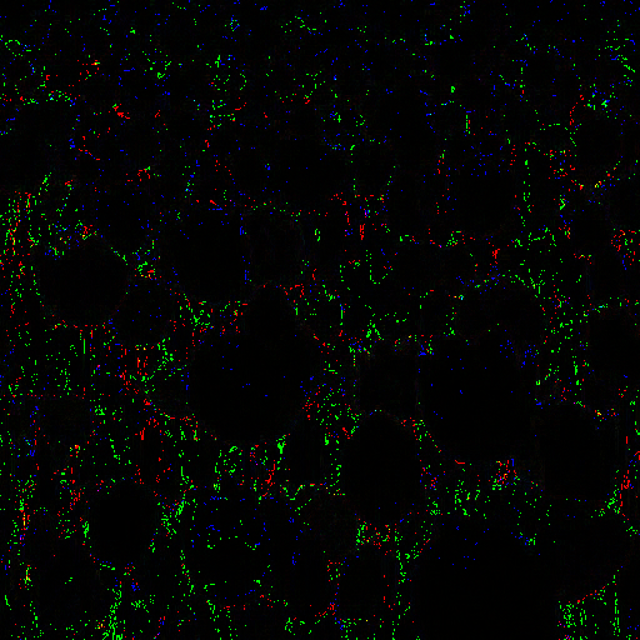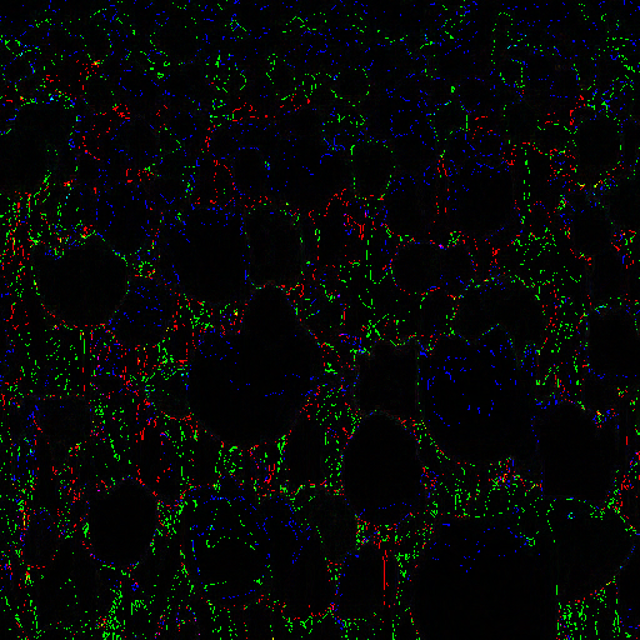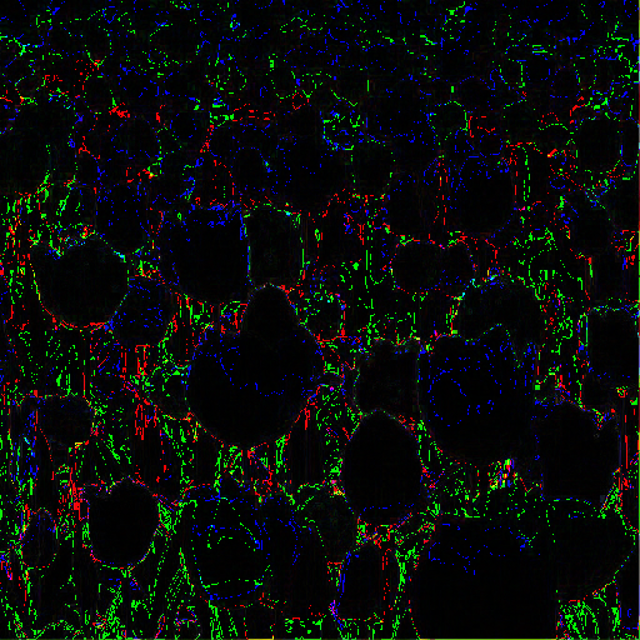| Origin with alpha channel | ComputeASTC 4x4 PSNR:38.08 | ComputeASTC 6x6 PSNR:34.92 |
|---|---|---|
 |
 |
 |
| Normal Map origin | ComputeASTC 4x4 PSNR: 43.74 |
|---|---|
 |
 |
2. 多图PSNR（峰值信噪比）对比
测试纹理：从GTA5里导出的220张纹理
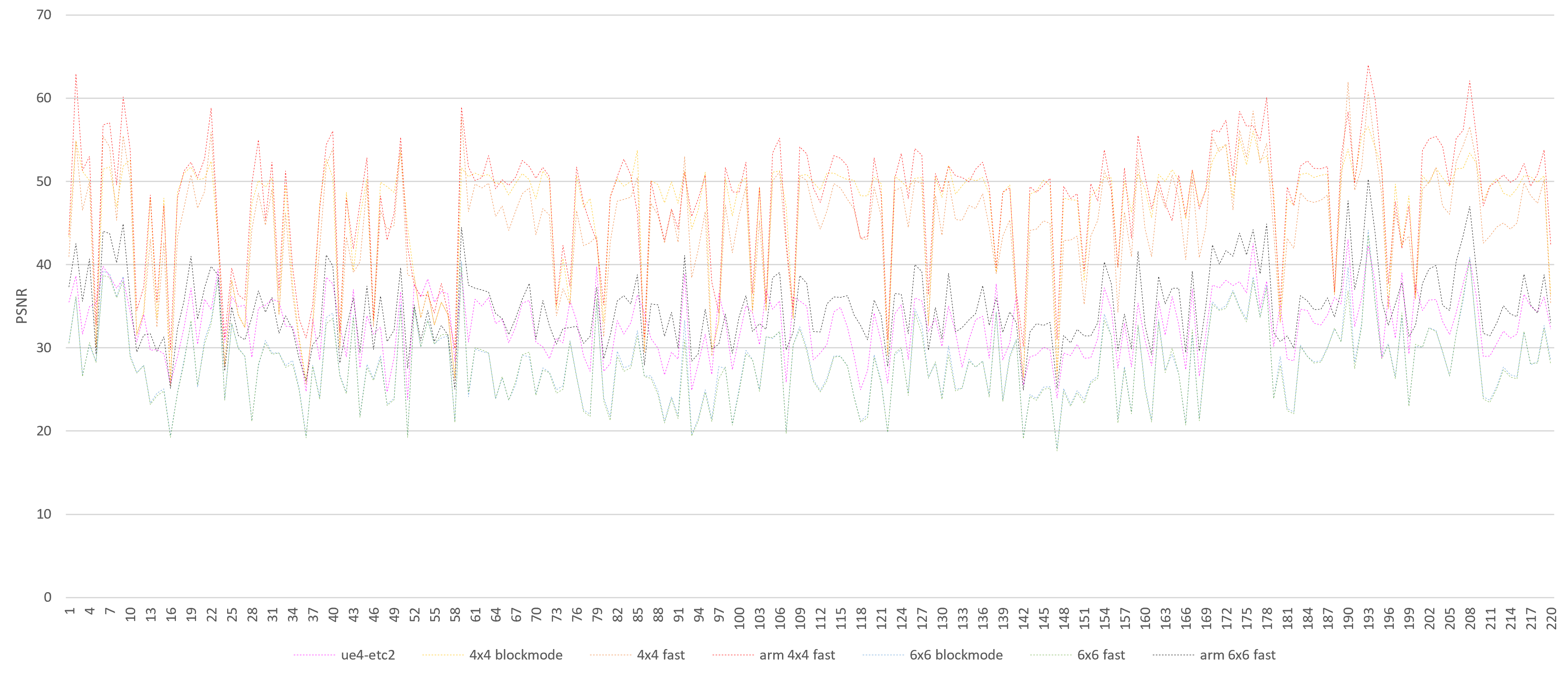
总体精度上远好于UE4-etc2，十分接近ARM-ASTC fast离线压缩。
各Endpoints算法的结果比较
各Endpoints算法的精度比较
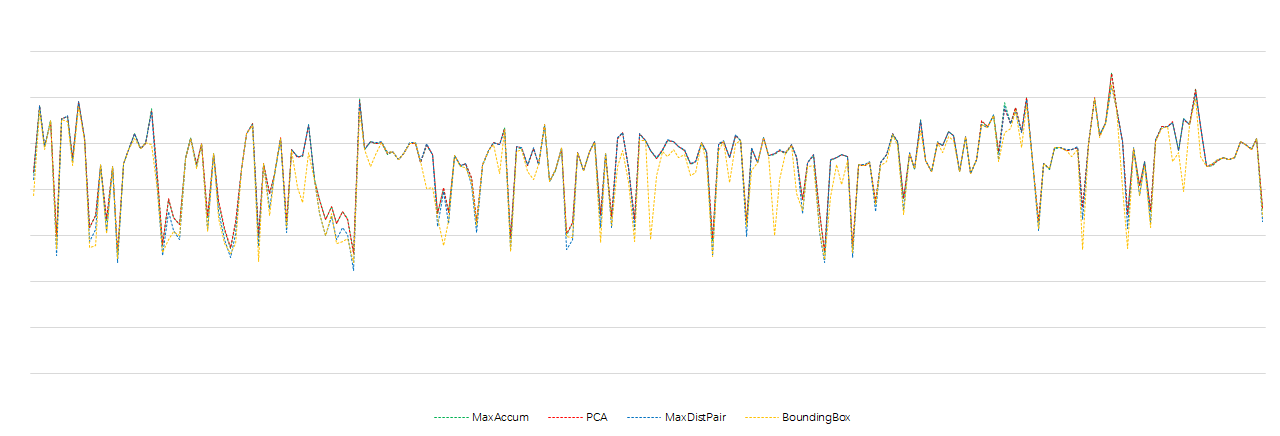
PCA的PSNR基本是最优的！MaxAccum与PCA非常接近
各Endpoints算法时间开销比较
压缩GPU时间开销(1024 4x4 fast on iphone12)：
| Method | Time(ms) |
|---|---|
| MaxAccum | 1.97 |
| PCA | 2.37 |
| BoundingBox | 1.61 |
| MaxDistPair | 8.25 |
MaxDistPair时间开销较大，BoundingBox精度较差，只考虑用MaxAccum或者PCA。 时间开销上除了MaxDistPair外差别不大，综合考虑用MaxAccum。
性能开销统计
| 全mips压缩 GPU时间开销(ms) | IPhone6s+ | IPhone12 |
|---|---|---|
| 512 4x4 fast | 0.75 | 0.53 |
| 512 6x6 fast | 1.13 | 0.52 |
| 1024 4x4 fast | 2.07 | 1.97 |
| 1024 6x6 fast | 3.87 | 1.88 |
| 2048 4x4 fast | * | 6.16 |
| 2048 6x6 fast | * | 6.88 |
| * | * | * |
| 512 4x4 blockmode | 5.72 | 4.35 |
| 512 6x6 blockmode | 10.51 | 7.44 |
| 1024 4x4 blockmode | * | * |
| 1024 6x6 blockmode | * | * |
同条件下与UE4.26 ETC2的对比：
| 方案 | GPU时间开销 |
|---|---|
| 1024 RGBA8-NoMips UE4-ETC2 @ IPhone12 | 0.85ms |
| 1024 4x4-NoMips ComputeASTC @ IPhone12 | 1.31ms |
ToDo
- 考虑通过聚类方式得到最优的partition划分，支持多partition以求提升大blocksize时的精度
[reference]
- https://www.khronos.org/registry/OpenGL/extensions/KHR/KHR_texture_compression_astc_hdr.txt
- https://www.khronos.org/registry/DataFormat/specs/1.2/dataformat.1.2.html#ASTC
- https://github.com/ARM-software/astc-encoder
- https://developer.arm.com/architectures/media-architectures/astc
- https://developer.nvidia.com/astc-texture-compression-for-game-assets
- http://delivery.acm.org/10.1145/2390000/2383812/supp/astc-supplemental-material.pdf
- https://developer.arm.com/-/media/Files/pdf/graphics-and-multimedia/Stacy_ASTC_white%20paper.pdf
- DANIEL OOM. Real-Time Adaptive Scalable Texture Compression for the Web
- Nystad.2012. Adaptive Scalable Texture Compression
- http://www.reedbeta.com/blog/understanding-bcn-texture-compression-formats/
- https://rockets2000.wordpress.com/2018/01/09/astc-partitions/
- Oskar. Compressing dynamically generated textures on the GPU
- https://community.arm.com/developer/tools-software/graphics/b/blog/posts/arm-unveils-details-of-astc-texture-compression-at-hpg-conference—part-1
- https://community.arm.com/developer/tools-software/graphics/b/blog/posts/astc-texture-compression-arm-pushes-the-envelope-in-graphics-technology
- https://zh.wikipedia.org/wiki/主成分分析
- https://zh.wikipedia.org/wiki/协方差矩阵
- https://www.cnblogs.com/pinard/p/6239403.html
- http://mlwiki.org/index.php/Power_Iteration
- https://www.researchgate.net/publication/259000525_Real-Time_DXT_Compression
- https://www.highperformancegraphics.org/previous/www_2012/media/Papers/HPG2012_Papers_Nystad.pdf
- https://developer.nvidia.com/blog/optimizing-compute-shaders-for-l2-locality-using-thread-group-id-swizzling
- https://solidpixel.github.io/2020/03/02/astc-compared.html
- https://prtsh.wordpress.com/2013/12/29/adaptive-scalable-texture-compression/