Uniform Sampling On Sphere

单位半球面上的均匀随机采样

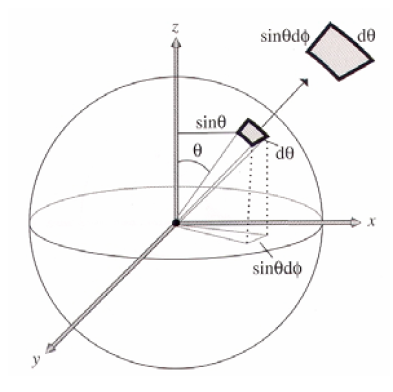
sphere_coordinate

在球面坐标系下，把球面微元看做简单矩形计算面积，可得球面微元面积： \(d\omega = sin({\theta})d{\theta} d{\phi}\) 其中\({\theta}\in[0,{\pi}/2],{\phi}\in [0, 2{\pi}]\)，而单位半球面的表面积为\(2\pi\)，均匀随机取一点，落在\(d\omega\)上的概率是\(d\omega/2{\pi}\)，

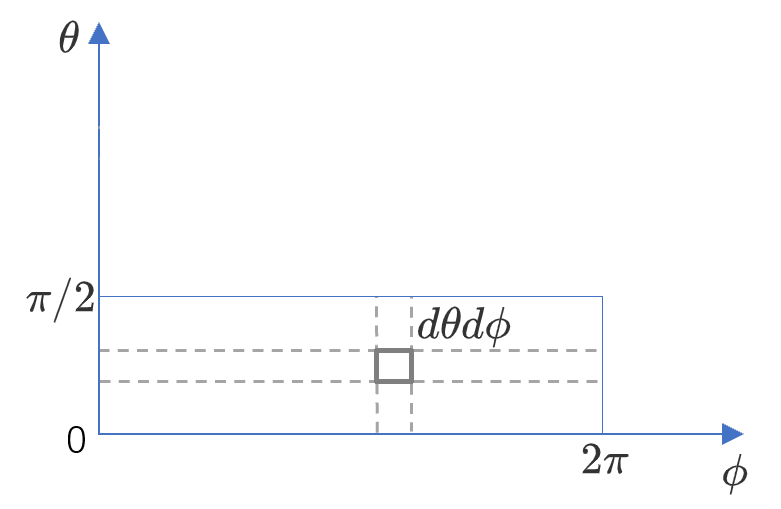
1638713535843

而\(d\omega\)对应在\(({\theta},{\phi})\)参数平面上的微小矩形区域\(d{\theta}d{\phi}\)内，对\(\theta,\phi\)独立随机采样，设联合概率密度函数为\(u(\theta)v(\phi)\)，那么采样点落在矩形区域\(d{\theta}d{\phi}\)上的概率是\(u(\theta)v(\phi)d{\theta}d{\phi}\)，即： \(d\omega/2{\pi} = u(\theta)v(\phi)d{\theta}d{\phi}\) 因为\(d\omega = sin({\theta})d{\theta} d{\phi}\)，于是：

\[\begin{equation}\begin{split} &sin({\theta})d{\theta} d{\phi}/2{\pi}=u(\theta)v(\phi)d{\theta}d{\phi}\\ &=> u(\theta)v(\phi)=sin({\theta})/2{\pi} \end{split}\end{equation}\]

计算边缘分布：

\[\begin{equation}\begin{split} &u(\theta)=\int_{0}^{2\pi} \frac{sin(\theta)}{2\pi}d{\phi}=sin(\theta)\\ &v(\phi)=\int_{0}^{\frac{\pi}{2}} \frac{sin(\theta)}{2\pi}d{\theta}=\frac{1}{2\pi} \end{split}\end{equation}\]

再根据从标准均匀分布计算指定分布的逆变换方法：

[1]先计算累积分布函数：

\[\begin{equation}\begin{split} &F_U(u)=\int_{0}^{u}sin(t)dt=1-cos(u)\\ &F_V(v)=\int_{0}^{v}\frac{1}{2\pi}dt=\frac{v}{2\pi} \end{split}\end{equation}\]

[2]取累积分布函数的反函数：

\[\begin{equation}\begin{split} &F_U^{-1}(u)=arccos(1-u)\\ &F_V^{-1}(v)=2{\pi}v \end{split}\end{equation}\]

[3]从标准均匀分布生成随机数\((U,V)\)，令：

\[\begin{equation}\begin{split} &{\Theta}=arccos(1-U)\\ &{\Phi}=2{\pi}V \end{split}\end{equation}\]

则\((\Theta,\Phi)\)是在\(({\theta},{\phi})\)参数平面上满足联合分布\(u(\theta)v(\phi)=sin({\theta})/2{\pi}\)的随机数，然后从\((\Theta,\Phi)\)计算出直角坐标系下的球面方向就是均匀分布的了。

代码：

import math
import random
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d as mplot3d

N = 10000

def sample_method_simple():
    theta = random.uniform(0, 0.5 * math.pi)
    phi = random.uniform(0, 2 * math.pi)
    cos_theta = math.cos(theta)
    sin_theta = math.sin(theta)
    return (math.cos(phi) * sin_theta, math.sin(phi) * sin_theta, cos_theta)

def sample_method_inversion_method():
    # gen uniform random in range(0, 1)
    u = random.uniform(0, 1)
    v = random.uniform(0, 1)
    # inversion method
    phi = v * 2 * math.pi
    cos_theta = 1 - u
    sin_theta = math.sqrt(1 - cos_theta * cos_theta)
    return (math.cos(phi) * sin_theta, math.sin(phi) * sin_theta, cos_theta)

def show_sample(method_func):
    x = [0] * N
    y = [0] * N
    z = [0] * N
    for i in range(N):
        r = method_func()
        x[i] = r[0]
        y[i] = r[1]
        z[i] = r[2]

    fig = plt.figure()
    ax = mplot3d.Axes3D(fig)
    ax.scatter(x, y, z, s = 0.2)
    ax.view_init(elev=80, azim = 0)
    ax.set_xlabel('X label')
    ax.set_ylabel('Y label')
    ax.set_zlabel('Z label')
    plt.show()

show_sample(sample_method_simple)
show_sample(sample_method_inversion_method)

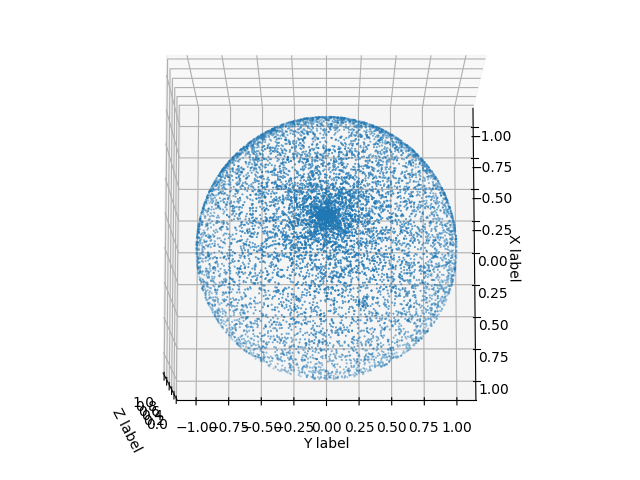
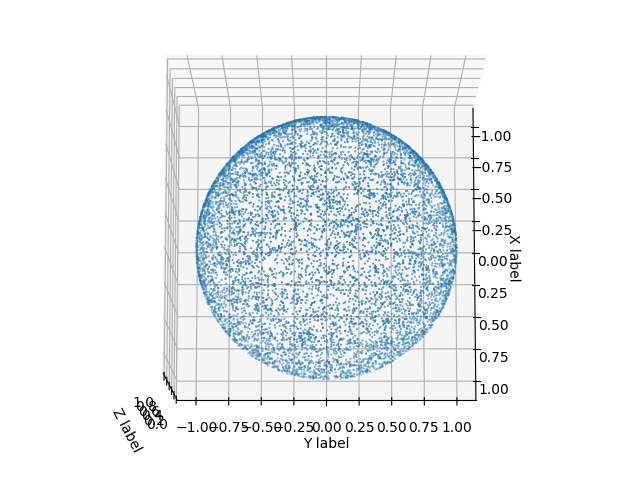
直接均匀随机采样\(({\theta},{\phi})\)	逆变换随机采样
采样点会在\(\theta=0\)附近出现聚集	采样点在球面上均匀分布

单位半球面上的均匀随机采样

Reference