Inverse Transform Sampling

逆变换采样(Inverse Transform Sampling or Inversion Method)是一种从标准均匀分布的随机数出发，通过变换生成按我们指定的概率密度分布的随机数的方法。[1][2]

问题

已知：随机变量\(X\)满足标准均匀分布，即\(X\sim U[0,1]\)，然后要求生成随机变量\(Y\)，使得\(Y\)满足概率密度分布\(f(y)\)，其中\(f(y)\)对应的累积分布函数\(F(y)\)是严格单调增的。

方法

生成标准均匀分布的随机数\(X\)
计算累积分布函数的反函数\(F^{-1}(y)\)
带入反函数生成随机变量\(Y=F^{-1}(X)\)，则\(Y\)满足概率密度分布\(f(y)\)

证明

对于随机变量\(X\)，如果满足标准均匀分布的话，对任给的\(a\in[0, 1]\)，有\(Pr(X≤a)=a\)，那么有：

\[Pr(X≤F(y))=F(y)\]

然后\(F(y)\)是值域\([0,1]\)上的严格单调递增函数，它一定存在反函数，且反函数也是严格单调递增的，于是：

\[Pr(F^{-1}(X)≤y)=F(y)\]

根据累积分布函数的定义\(F(y) = Pr(X≤y)\)，上式表明\(F^{-1}(X)\)是个满足累积分布函数\(F(y)\)的随机数，证毕。

例子

从标准均匀分布随机数生成满足指数分布的随机数，指数分布 \(X\sim exp(1)\)

\[f(x)=\begin{cases}e^{-x} & x\geq0 \\0 & x<0 \end{cases}\]

累积分布函数： \(F(x)=\begin{cases}1-e^{-x} & x\geq0 \\0 & x<0 \end{cases}\)
\(F(x)\)的反函数：\(F^{-1}(x)=-ln(1-x)\)，其中\(x\in[0,1)\)
\(X\)满足\(U[0,1]\)分布，则\(-ln(1-X)\)满足指数分布。

python代码：

import math
import random
import matplotlib.pyplot as plt

N = 200000
Q = 20
S = 10

rand_counts = [0] * Q * S     # random value counter, the counter proportion is the pdf(probability distribution function)

for i in range(N):
    r = random.uniform(0, 1)  # gen uniform random in range(0, 1)
    r = -math.log(1 - r)    # inverse transform to get exp distribution
    c = (int)(r * S)
    if c < Q * S:
        rand_counts[c] = rand_counts[c] + 1

total = sum(rand_counts)
print ("total = ", total)

x = [0] * Q * S
y = [0] * Q * S
for i in range(Q * S):
	x[i] = i / S
	y[i] = rand_counts[i] * S / total
plt.plot(x,y)
plt.show()

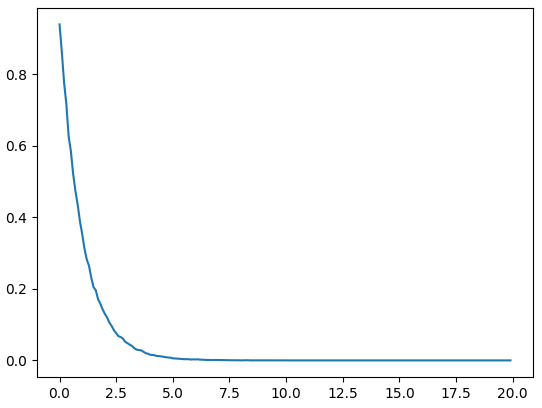
基本符合\(y=e^{-x}\)

exp_rand

问题

方法

证明

例子

Reference