习惯约定

  • 记号
  1. L 光照方向
  2. N 法线方向
  3. V 视角方向
  4. T 切线方向
  5. H 半角向量
  • 无论入射光，反射光，其方向向量都约定为从表面点出发向外。

基于物理的渲染

能量守恒

说光照模型是能量守恒的，具体是指BRDF（双向反射分布函数）\(f_r(p,\omega_i,\omega_o)\)满足： \[∀\omega_i有 \int_{Ω}f_r(p,\omega_i,\omega_o)(n⋅\omega_i)d\omega_i≤1\]

光路可逆（互异性）

\[f_r(p,\omega_i,\omega_o)=f_r(p,\omega_o,\omega_i)\]

迪斯尼原则的PBR

  • 可实时计算
  • 参数少且简单直观
  • 能涵盖绝大多数材质表现

Direct lighting

Cook-Torrance微平面模型

  1. 法线分布函数项Normal distribution function (specular D)
  2. 几何遮蔽项Geometric shadowing (specular G)
  3. 菲涅尔项Fresnel (specular F)

渲染方程：

\[L_o(p,\omega_{o})=k_d∫_{ \Omega}(\frac{\rho}{\pi})L_{i}(p,\omega_{i})n⋅\omega_{i}d\omega_{i} + k_s∫_{ \Omega}(\frac{DFG}{4.(\omega_{o}.n).(\omega_{i}.n)})L_{i}(p,\omega_{i})n⋅\omega_{i}d\omega_{i}\]

其中\(k_d\)对应diffuse部分，\(k_s\)对应specular部分

Indirect lighting(IBL)

Indirect diffuse lighting

img

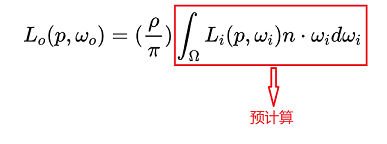
预积分计算irradiance map

从radiance map（环境立方体贴图）预积分计算出irradiance map，环境立方体贴图的每个像素代表一个环境光源，积分计算中，以给定点的法线方向确定的上半球面为积分域，而上式中的积分值仅与法线\(n\)有关，因此我们可以针对每一个法线取值预计算出积分值，然后保存到贴图中以供实时渲染时查询使用，这张贴图称为irradiance map，这实际上是对原环境立方体贴图做了一个核为\(n⋅\omega_{i}\)的一个卷积计算，如下图所示。

irradiance

Left the radiance map, right the irradiance map (Lambert rendering equation)

Monte Carlo计算定积分

要计算定积分：

\[F = \int_{\Omega}f(x)dx\]

可以采用对被积函数的随机采样值的统计平均来近似估算积分： \(F \approx F_N=\frac{1}{N} \sum\limits_{i=1}^{N} \frac{f(x_i)}{p(x_i)}\)

其中\(p(x_i)\)概率密度函数。

可以证明统计值的数学期望：\(E[F_N] = F\)，也即\(F_N\)是\(F\)的一个无偏估计。

球面均匀随机采样

  • 对给定的方向，以其为中心生成均匀随机分布的半球面采样点。
  • 非差异化随机序列（hammersley序列）

半球面上的积分离散采样

漫反射项积分 \(L_o(p,\omega_{o})=k_d(\frac{\rho}{\pi})∫_{ \Omega}L_{i}(p,\omega_{i})n⋅\omega_{i}d\omega_{i}\)

转到球面坐标下\(d\omega_{i}=sin(\theta)d{\theta}d{\phi}\)，其中 \({\theta}\in[0,{\pi}/2],{\phi}\in [0, 2{\pi}]\) ，为了球面均匀采样，再做积分换元

\[\begin{cases} u = 1 - cos{\theta}\\ v = \frac{\phi}{2{\pi}} \end{cases}\]

得到：

\[\begin{equation} \begin{split} L_o(p,\omega_{o})=k_{d}(\frac{\rho}{\pi})\int_{0}^{2{\pi}}\int_{0}^{\frac{\pi}{2}}L_{i}(p,\omega_{i})n⋅\omega_{i}sin{\theta}d{\theta}d{\phi} \\ =k_{d}(\frac{\rho}{\pi})\int_{0}^{1}\int_{0}^{1}L_{i}(p,\omega_{i})n⋅\omega_{i}sin{\theta}Jdudv \end{split} \end{equation}\]

其中\(J\)是多重积分换元的雅可比行列式：

\[J=\left| \begin{array}{cccc} \frac{\partial {\theta}}{\partial {u}} & \frac{\partial {\theta}}{\partial {v}} \\ \frac{\partial {\phi}}{\partial {u}} & \frac{\partial {\phi}}{\partial {v}} \\ \end{array} \right| = \frac{2{\pi}}{\sqrt{1-(1-u)^2}} = \frac{2{\pi}}{sin\theta}\]

代入得：

\[L_o(p,\omega_{o})=k_{d}(2{\rho})\int_{0}^{1}\int_{0}^{1}L_{i}(p,\omega_{i})n⋅\omega_{i}dudv\]

进行Monte-Carlo随机采样，取均匀随机分布，概率密度函数(pdf)为常数1，从\(u,v\)计算出 \({\theta,\phi}\) ，然后计算方向向量\(\omega_{i}=(cos{\phi}sin{\theta}, sin{\phi}sin{\theta}, cos{\theta})\)，则Monte Carlo积分格式为：

\[L_o(p,\omega_{o}) \approx k_{d}{\rho}[\frac{2}{N}\sum\limits_{i=1}^N L_{i}(p,\omega_{i})n⋅\omega_{i}]\]

注意：albedo值\({\rho}\)和漫反射系数\(k_d\)不预计算到irradiance map中，预计算已经除过了\(\pi\) 。

漫反射系数的计算

specular 系数就是用F，对应的漫反射系数，要考虑金属度

\[\begin{cases} &K_s = F\\ &K_d = (1 - F)(1 - metallic) \end{cases}\]

Indirect specular lighting

利用分离和近似将积分拆分为两部分的乘积：

  • 第一部分是预滤波环境贴图

它类似于辐照度图，是预先计算的环境卷积贴图，但这次考虑了粗糙度。因为随着粗糙度的增加，参与环境贴图卷积的采样向量会更分散，导致反射更模糊，所以对于卷积的每个粗糙度级别，按顺序把模糊后的结果存储在预滤波贴图的mipmap中，roughness越小对应于mip层级越高。 prefilter_mips

  • 第二部分是NdotL和roughness的函数，UE4预计算为lut，也可以用函数拟合方式计算（ 使命召唤黑色行动2）

    integrateBRDF_lut
    IntegrateBRDF的lut，横轴是dot(N,L)，纵轴是roughness

《使命召唤黑色行动2》用函数拟合来实时计算

// 第二部分的拟合函数
float2 EnvBRDFApprox_BlackOp2(float Roughness, float NV)
{
    float g = 1 - Roughness;
    float4 t = float4(1/0.96, 0.475, (0.0275 - 0.25*0.04)/0.96, 0.25);
    t *= float4(g, g, g, g);
    t += float4(0, 0, (0.015 - 0.75*0.04)/0.96, 0.75);
    float A = t.x * min(t.y, exp2(-9.28 * NV)) + t.z;
    float B = t.w;
    return float2 ( t.w-A,A);
}

//UE4 在 黑色行动2 上的修改版本
float2 EnvBRDFApprox_UE4(float Roughness, float NoV )
{
    // [ Lazarov 2013, "Getting More Physical in Call of Duty: Black Ops II" ]
    // Adaptation to fit our G term.
    const float4 c0 = { -1, -0.0275, -0.572, 0.022 };
    const float4 c1 = { 1, 0.0425, 1.04, -0.04 };
    float4 r = Roughness * c0 + c1;
    float a004 = min( r.x * r.x, exp2( -9.28 * NoV ) ) * r.x + r.y;
    float2 AB = float2( -1.04, 1.04 ) * a004 + r.zw;
    return AB;
}

IBL error source

  1. 分离和近似引入的误差
  2. v=n=r 假设引入的误差，这个比分离和引起的误差更大些

important tricks

  • BRDF的几何遮蔽项（SpecularG）在计算IBL和直接光时略有不同：
\[\begin{cases} &K_{direct}=\frac{(roughness + 1)^2}{8}\\ &K_{IBL}=\frac{(roughness)^2}{2} \end{cases}\]
  • Fresnel项在计算IBL时和计算直接光时的有所区别：

在计算IBL时，由于环境光来自半球内围绕法线 N 的所有方向，因此没有一个确定的半向量来计算菲涅耳效应。为了模拟菲涅耳效应，我们用法线和视线之间的夹角计算菲涅耳系数。然而，之前我们是以受粗糙度影响的微表面半向量作为菲涅耳公式的输入，但我们目前没有考虑任何粗糙度，表面的反射率总是会相对较高。间接光和直射光遵循相同的属性，因此我们期望较粗糙的表面在边缘反射较弱，引入粗糙度，降低反射。

\[\begin{cases} &F_{fresnel} = f_0+(1-f_0)(1-h \cdot v)^5\\ &F_{fresnel\_roughness} = f_0+(max(f0, 1 - roughness) - f_0)(1-n \cdot v)^5 \end{cases}\]

  • 最小的roughness值：roughness为0，对应着完全的反射，对于非面积光源，会产生无穷大的反射值（能量全部集中到了面积为0的一点上）, UE4的SM5下roughness默认最小值为0.2

  • F：菲涅尔系数，是光线发生反射与折射的比例，当光线垂直进入表面时的菲涅尔系数记为F0，F0是可以实际测量出来的， 不同的材质，这个F0是不同的，F0越大，感觉是越明亮，金属材质通常F0比较大，而且是有颜色的（不同频率的光，对应菲涅尔系数不同），非金属材质最低也有一点点反射，就取(0.04, 0.04, 0.04)，渲染中通常用一个权重系数（金属度）在非金属材质的最小菲涅尔系数和具有最强金属性的材质菲涅尔系数（自身漫反射颜色）之间进行线性插值得到F0.
  • 实际计算中，高光项并没有再乘上\(k_s\).

[reference]

  1. https://learnopengl.com/PBR
  2. [Brian Karis] Real Shading in Unreal Engine 4
  3. [Naty Hoffffman] Background: Physics and Math of Shading
  4. https://google.github.io/filament/Filament.html
  5. http://www.codinglabs.net/article_physically_based_rendering.aspx
  6. https://seblagarde.wordpress.com/2011/08/17/hello-world/
  7. http://www.sztemple.cc/articles/pbr理论体系整理（三）：ibl
  8. [Schlick94] Christophe Schlick. 1994. An Inexpensive BRDF Model for Physically-Based Rendering. Computer Graphics Forum, 13 (3), 233–246.
  9. https://en.wikipedia.org/wiki/Inverse_transform_sampling 10.https://www.cnblogs.com/timlly/p/10631718.html